初探动态规划
初探动态规划
「动态规划 dynamic programming」是一个重要的算法范式,它将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率。
在本节中,我们从一个经典例题入手,先给出它的暴力回溯解法,观察其中包含的重叠子问题,再逐步导出更高效的动态规划解法。
"爬楼梯"
给定一个共有 $n$ 阶的楼梯,你每步可以上 $1$ 阶或者 $2$ 阶,请问有多少种方案可以爬到楼顶。
如下图所示,对于一个 阶楼梯,共有 种方案可以爬到楼顶。
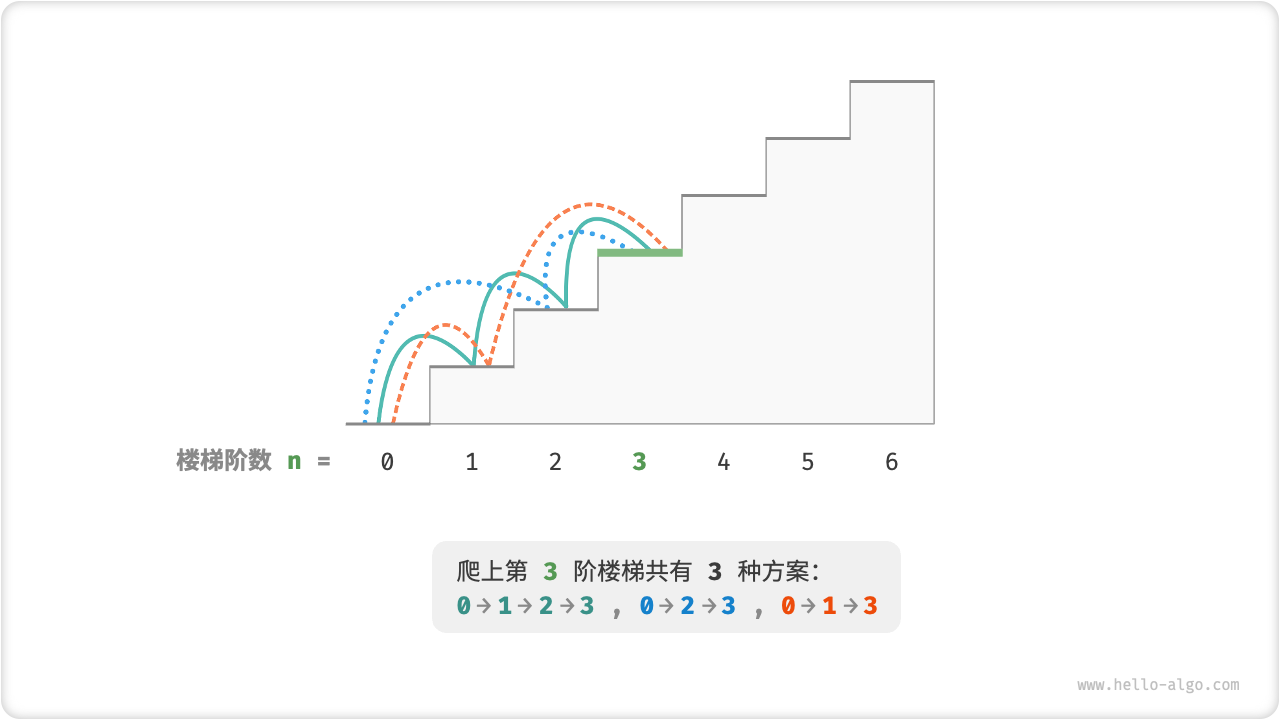
本题的目标是求解方案数量,我们可以考虑通过回溯来穷举所有可能性。具体来说,将爬楼梯想象为一个多轮选择的过程:从地面出发,每轮选择上 阶或 阶,每当到达楼梯顶部时就将方案数量加 ,当越过楼梯顶部时就将其剪枝。
[file]{climbing_stairs_backtrack}-[class]{}-[func]{climbing_stairs_backtrack}
方法一:暴力搜索
回溯算法通常并不显式地对问题进行拆解,而是将问题看作一系列决策步骤,通过试探和剪枝,搜索所有可能的解。
我们可以尝试从问题分解的角度分析这道题。设爬到第 阶共有 种方案,那么 就是原问题,其子问题包括:
由于每轮只能上 阶或 阶,因此当我们站在第 阶楼梯上时,上一轮只可能站在第 阶或第 阶上。换句话说,我们只能从第 阶或第 阶前往第 阶。
由此便可得出一个重要推论:爬到第 阶的方案数加上爬到第 阶的方案数就等于爬到第 阶的方案数。公式如下:
这意味着在爬楼梯问题中,各个子问题之间存在递推关系,原问题的解可以由子问题的解构建得来。下图展示了该递推关系。
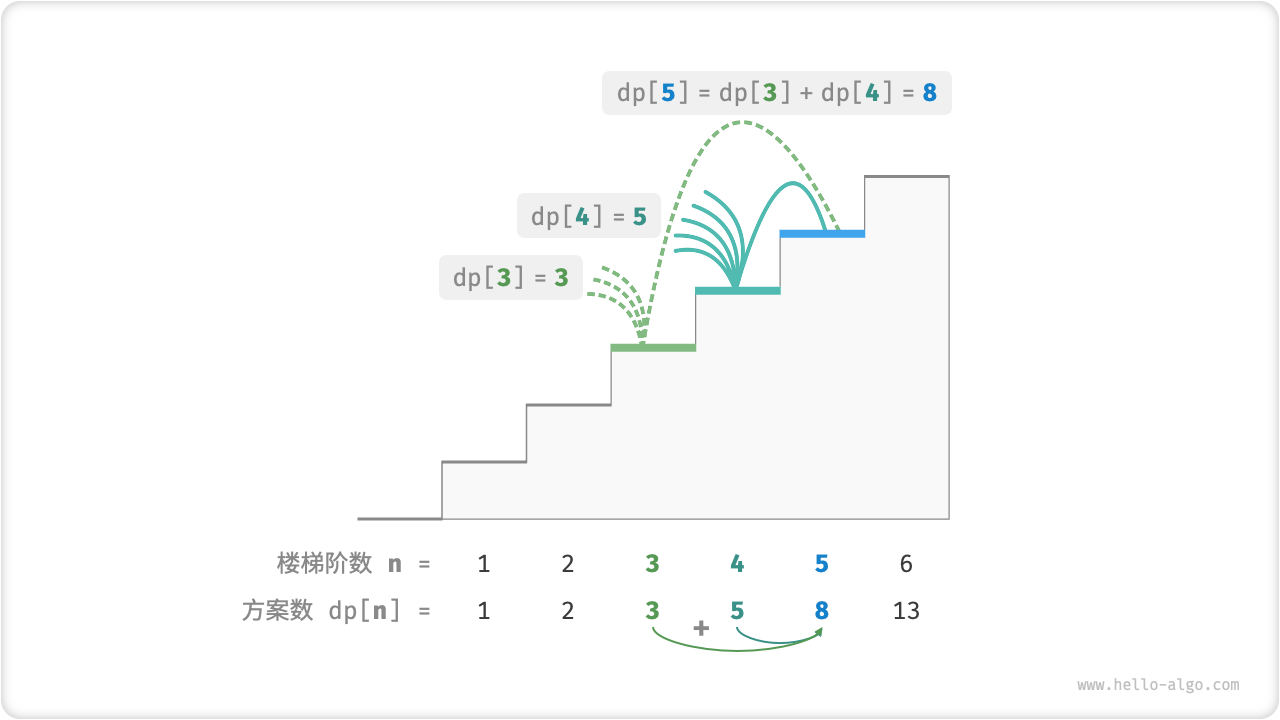
我们可以根据递推公式得到暴力搜索解法。以 为起始点,递归地将一个较大问题拆解为两个较小问题的和,直至到达最小子问题 和 时返回。其中,最小子问题的解是已知的,即 、 ,表示爬到第 、 阶分别有 、 种方案。
观察以下代码,它和标准回溯代码都属于深度优先搜索,但更加简洁。
[file]{climbing_stairs_dfs}-[class]{}-[func]{climbing_stairs_dfs}
下图展示了暴力搜索形成的递归树。对于问题 ,其递归树的深度为 ,时间复杂度为 。指数阶属于爆炸式增长,如果我们输入一个比较大的 ,则会陷入漫长的等待之中。
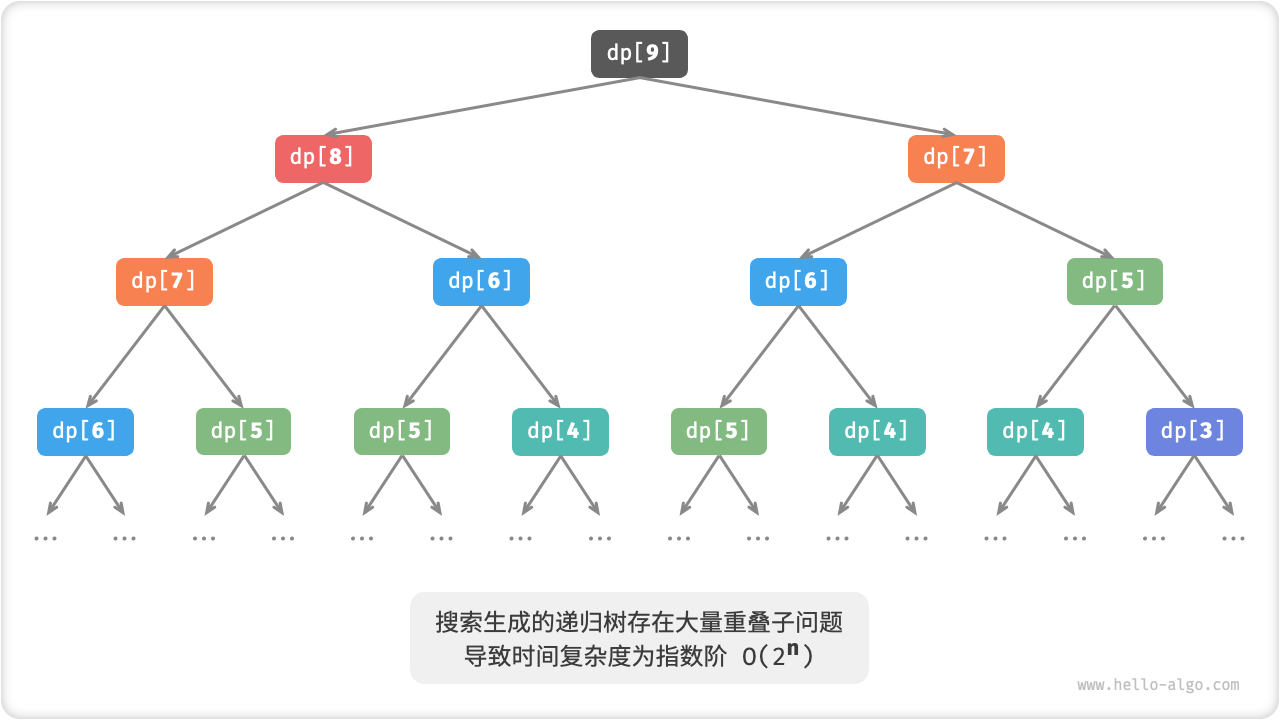
观察上图,指数阶的时间复杂度是由于“重叠子问题”导致的。例如 被分解为 和 , 被分解为 和 ,两者都包含子问题 。
以此类推,子问题中包含更小的重叠子问题,子子孙孙无穷尽也。绝大部分计算资源都浪费在这些重叠的问题上。
方法二:记忆化搜索
为了提升算法效率,我们希望所有的重叠子问题都只被计算一次。为此,我们声明一个数组 mem 来记录每个子问题的解,并在搜索过程中将重叠子问题剪枝。
- 当首次计算 时,我们将其记录至
mem[i],以便之后使用。 - 当再次需要计算 时,我们便可直接从
mem[i]中获取结果,从而避免重复计算该子问题。
[file]{climbing_stairs_dfs_mem}-[class]{}-[func]{climbing_stairs_dfs_mem}
观察下图,经过记忆化处理后,所有重叠子问题都只需被计算一次,时间复杂度被优化至 ,这是一个巨大的飞跃。
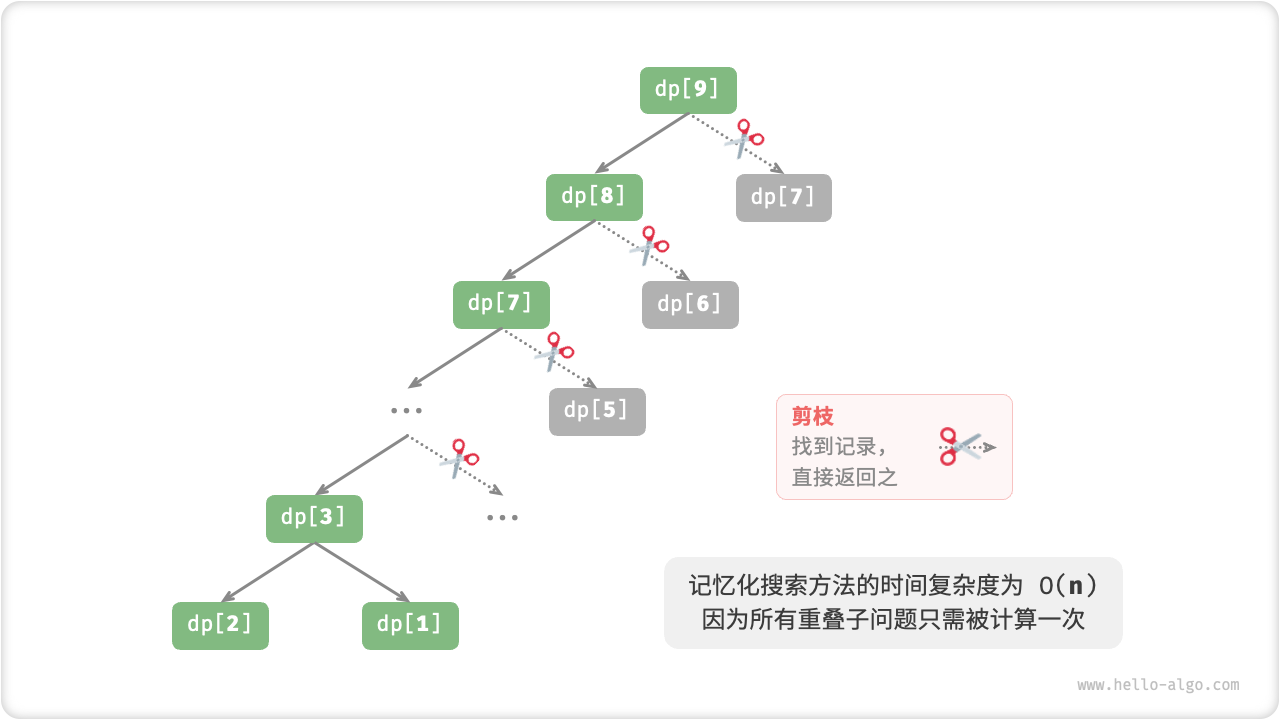
方法三:动态规划
记忆化搜索是一种“从顶至底”的方法:我们从原问题(根节点)开始,递归地将较大子问题分解为较小子问题,直至解已知的最小子问题(叶节点)。之后,通过回溯将子问题的解逐层收集,构建出原问题的解。
与之相反,动态规划是一种“从底至顶”的方法:从最小子问题的解开始,迭代地构建更大子问题的解,直至得到原问题的解。
由于动态规划不包含回溯过程,因此只需使用循环迭代实现,无须使用递归。在以下代码中,我们初始化一个数组 dp 来存储子问题的解,它起到了记忆化搜索中数组 mem 相同的记录作用。
[file]{climbing_stairs_dp}-[class]{}-[func]{climbing_stairs_dp}
下图模拟了以上代码的执行过程。
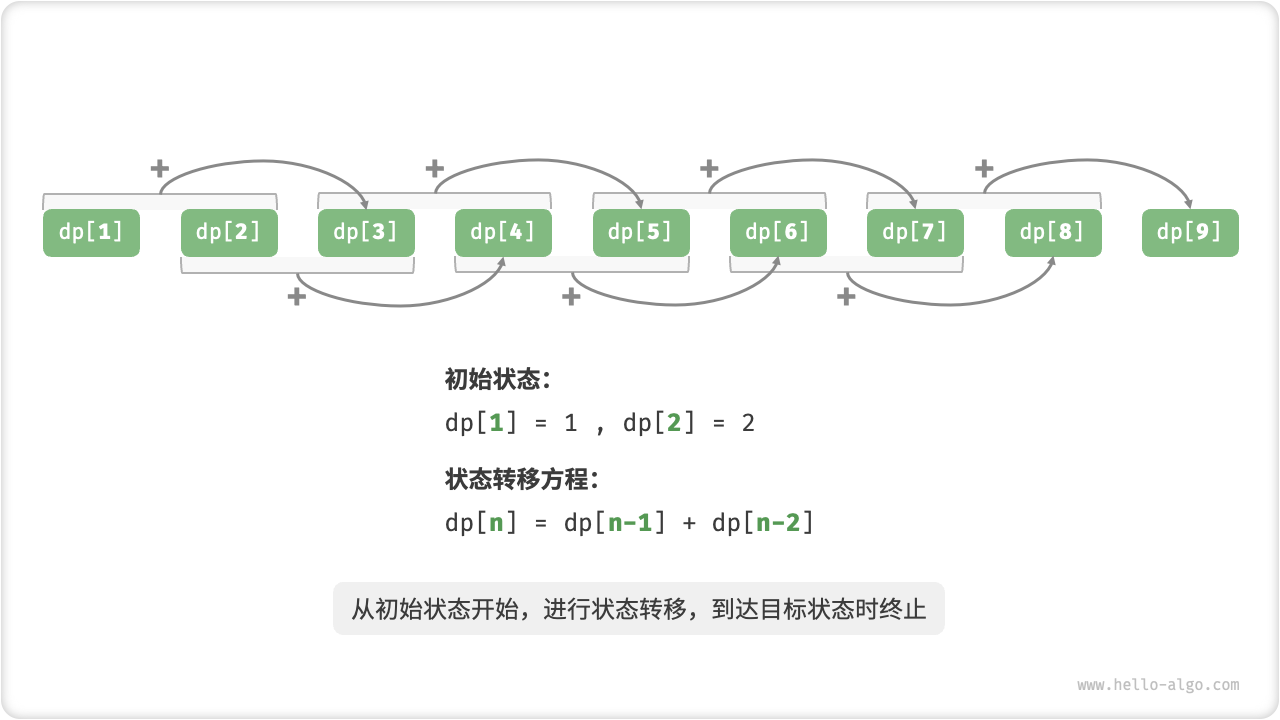
与回溯算法一样,动态规划也使用“状态”概念来表示问题求解的某个特定阶段,每个状态都对应一个子问题以及相应的局部最优解。例如,爬楼梯问题的状态定义为当前所在楼梯阶数 。
根据以上内容,我们可以总结出动态规划的常用术语。
- 将数组
dp称为「 表」, 表示状态 对应子问题的解。 - 将最小子问题对应的状态(即第 和 阶楼梯)称为「初始状态」。
- 将递推公式 称为「状态转移方程」。
空间优化
细心的你可能发现,由于 只与 和 有关,因此我们无须使用一个数组 dp 来存储所有子问题的解,而只需两个变量滚动前进即可。
[file]{climbing_stairs_dp}-[class]{}-[func]{climbing_stairs_dp_comp}
观察以上代码,由于省去了数组 dp 占用的空间,因此空间复杂度从 降低至 。
在动态规划问题中,当前状态往往仅与前面有限个状态有关,这时我们可以只保留必要的状态,通过“降维”来节省内存空间。这种空间优化技巧被称为“滚动变量”或“滚动数组”。
