# 二分查找

「二分查找 binary search」是一种基于分治策略的高效搜索算法。它利用数据的有序性，每轮减少一半搜索范围，直至找到目标元素或搜索区间为空为止。

给定一个长度为 $n$ 的数组 `nums` ，元素按从小到大的顺序排列，数组不包含重复元素。请查找并返回元素 `target` 在该数组中的索引。若数组不包含该元素，则返回 $-1$ 。

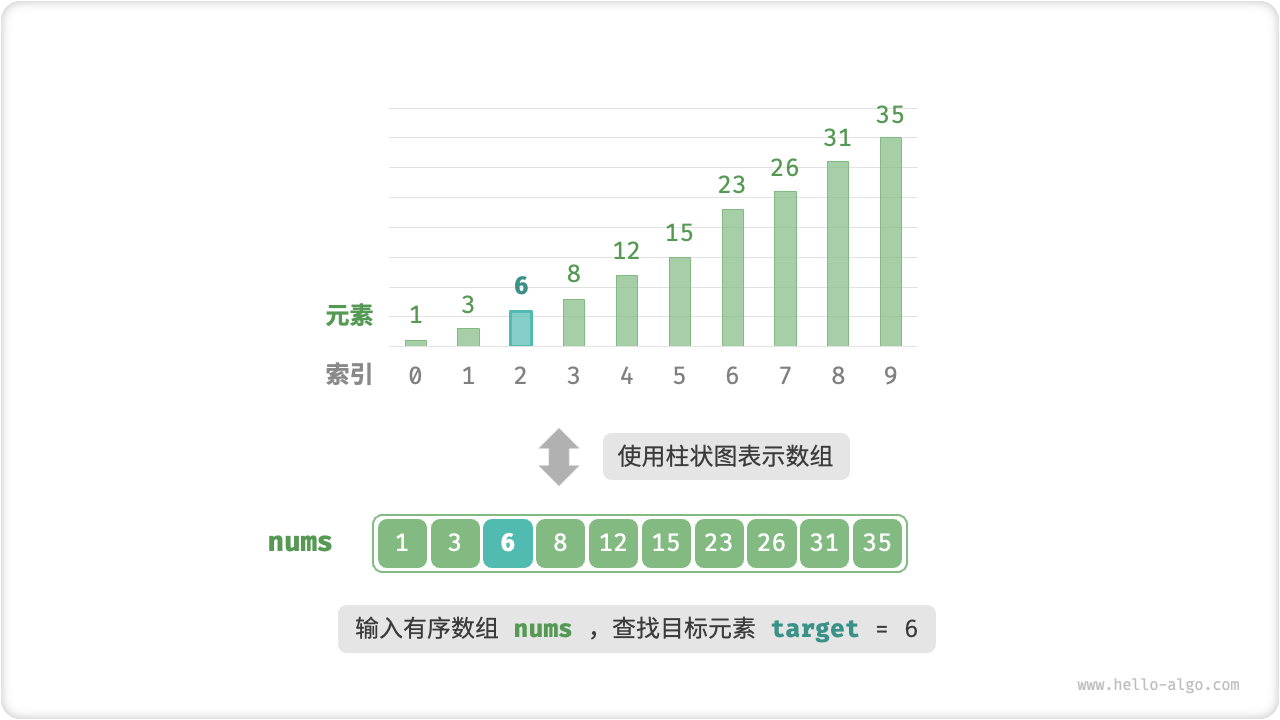
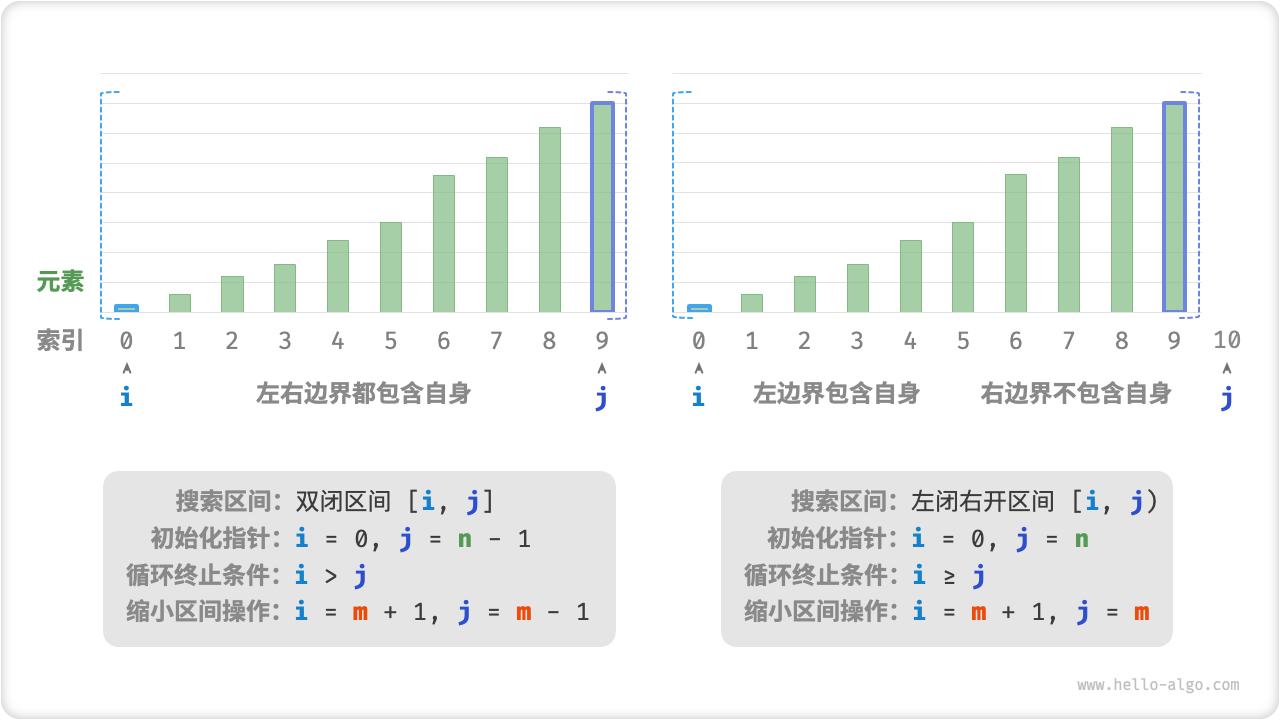
如下图所示，我们先初始化指针 $i = 0$ 和 $j = n - 1$ ，分别指向数组首元素和尾元素，代表搜索区间 $[0, n - 1]$ 。请注意，中括号表示闭区间，其包含边界值本身。

接下来，循环执行以下两步。

1. 计算中点索引 $m = \lfloor {(i + j) / 2} \rfloor$ ，其中 $\lfloor \: \rfloor$ 表示向下取整操作。
2. 判断 nums[m] 和 target 的大小关系，分为以下三种情况。
   1. 当 nums[m] < target 时，说明 target 在区间 $[m + 1, j]$ 中，因此执行 $i = m + 1$ 。
   2. 当 nums[m] > target 时，说明 target 在区间 $[i, m - 1]$ 中，因此执行 $j = m - 1$ 。
   3. 当 nums[m] = target 时，说明找到 target ，因此返回索引 $m$ 。

若数组不包含目标元素，搜索区间最终会缩小为空。此时返回 $-1$ 。

=== "<1>"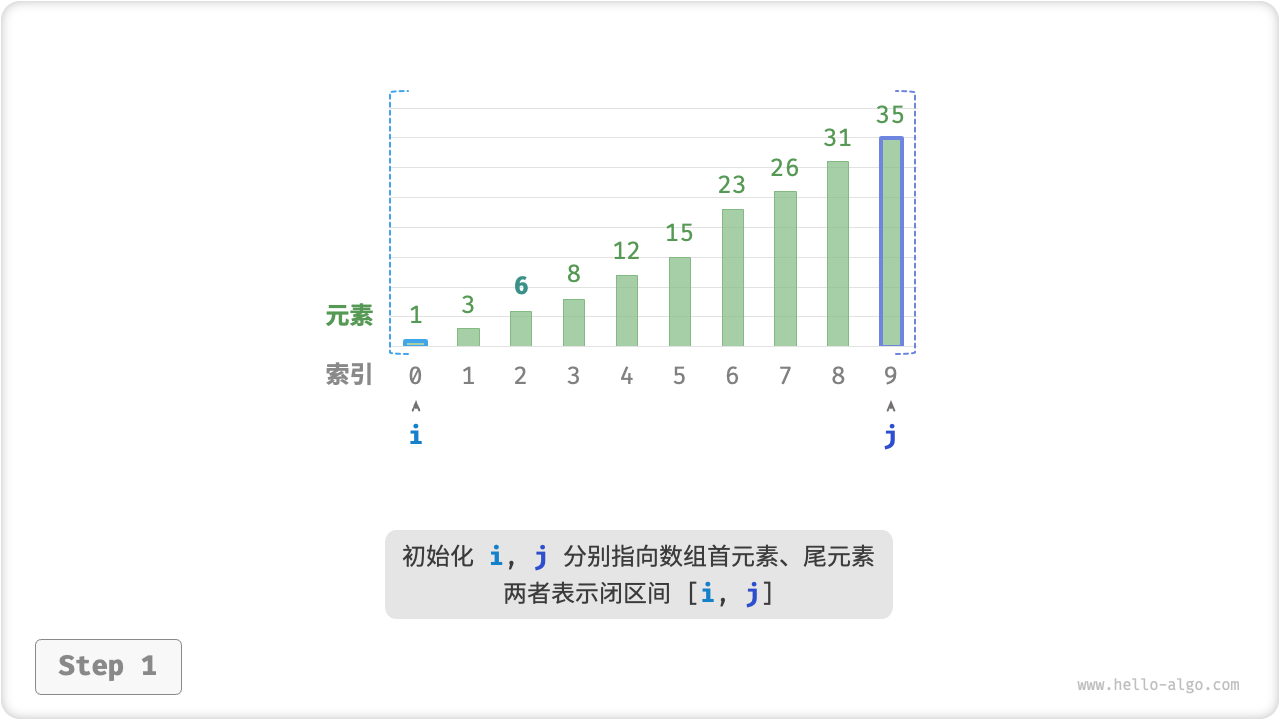

=== "<2>"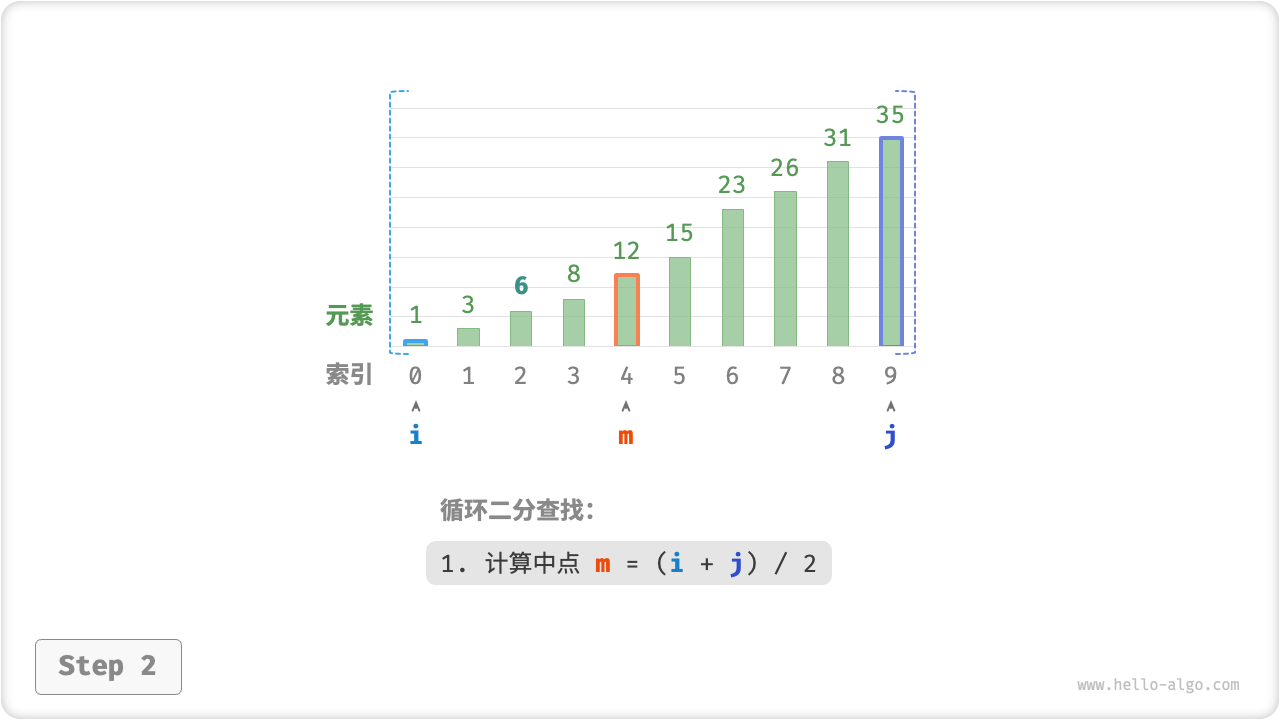

=== "<3>"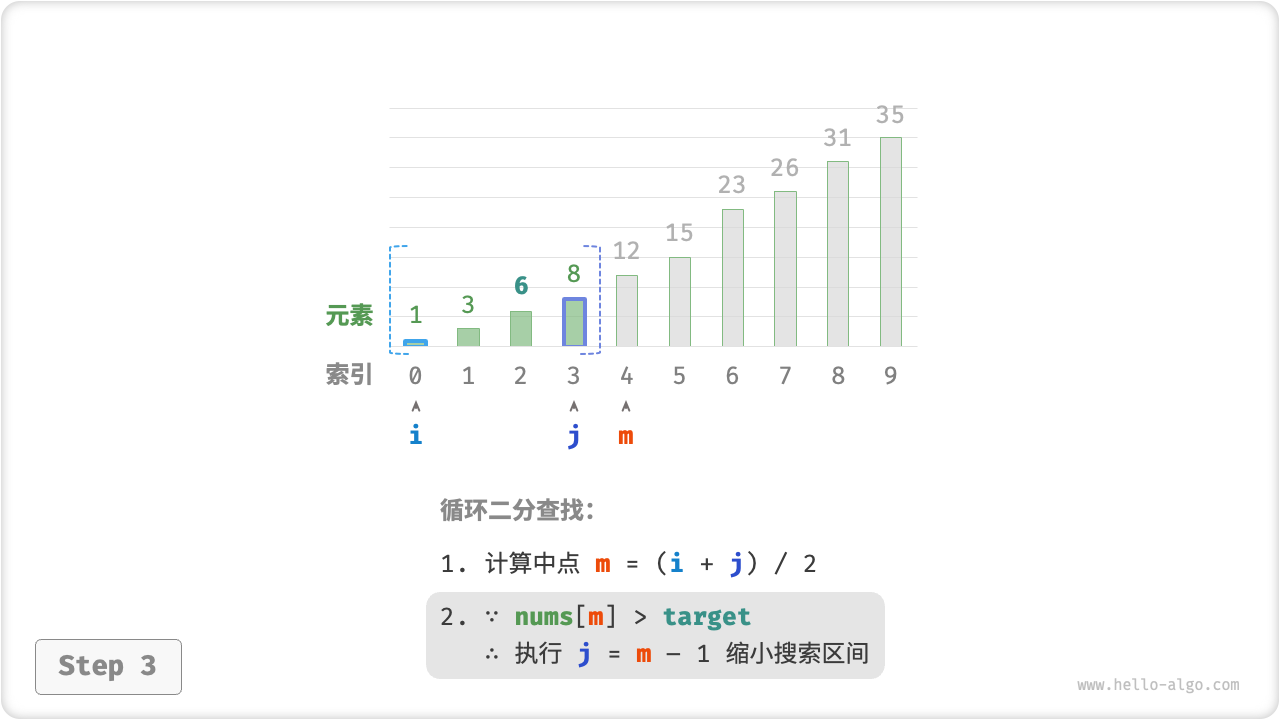

=== "<4>"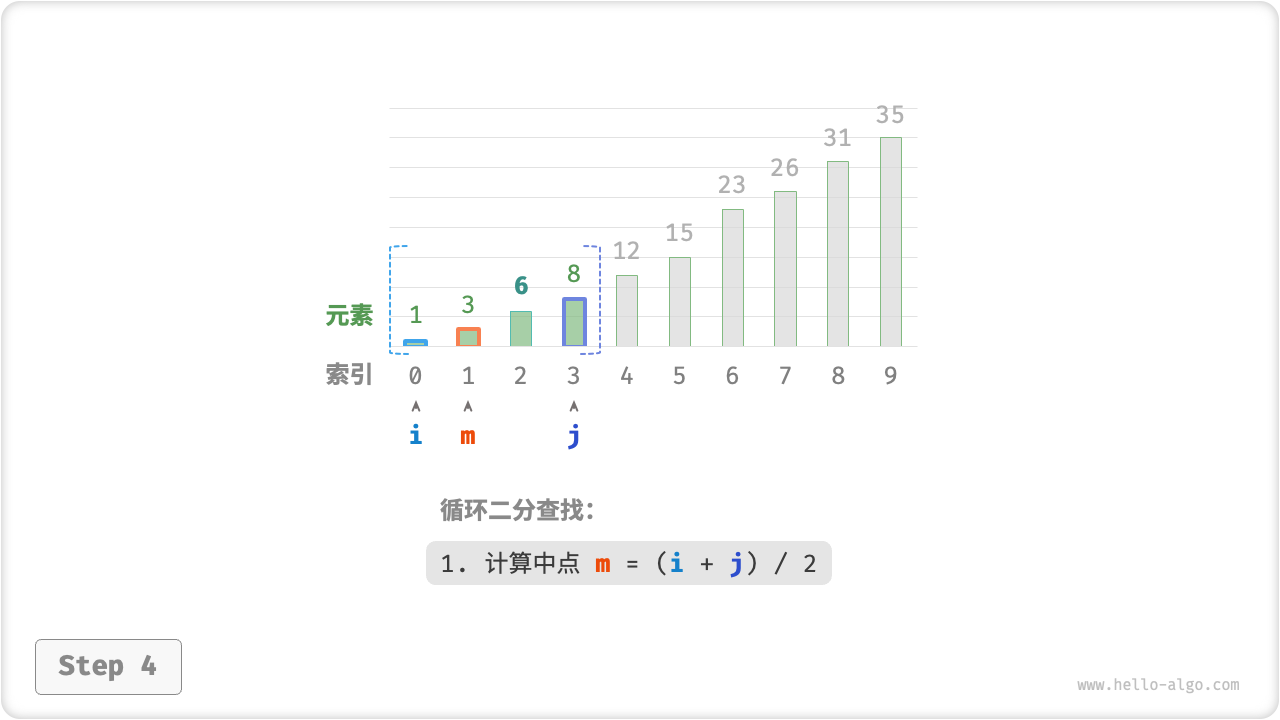

=== "<5>"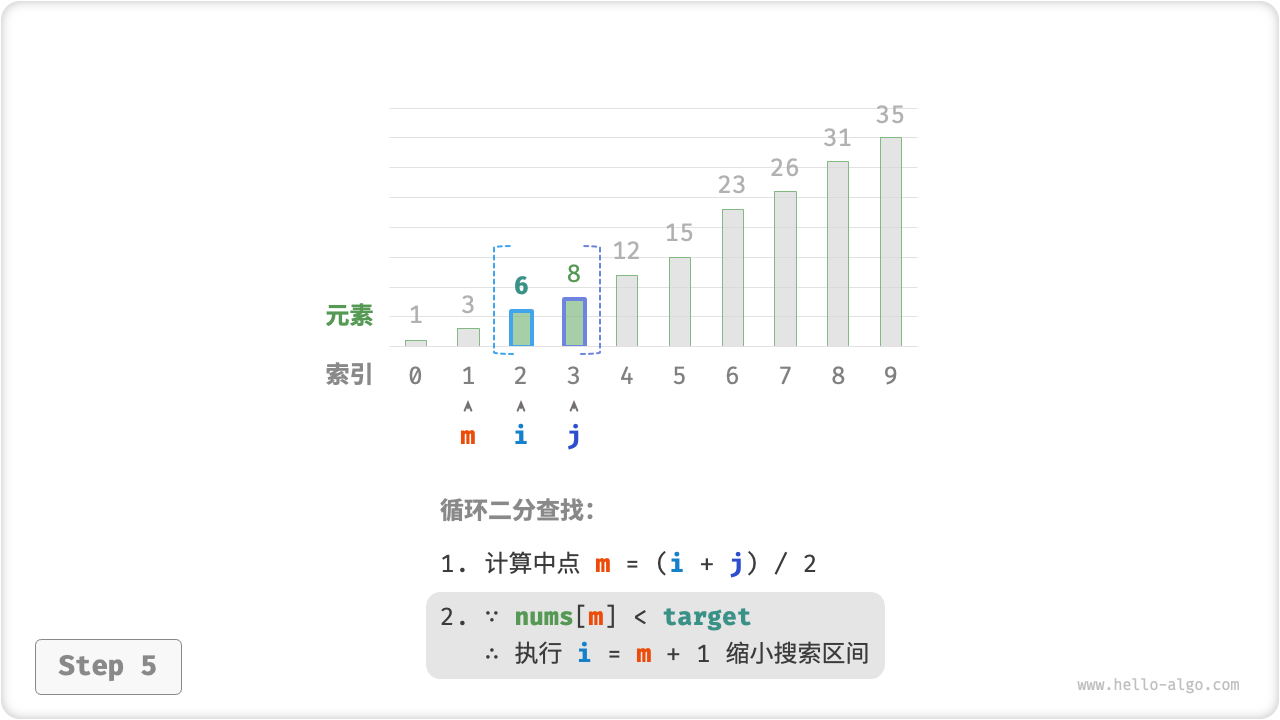

=== "<6>"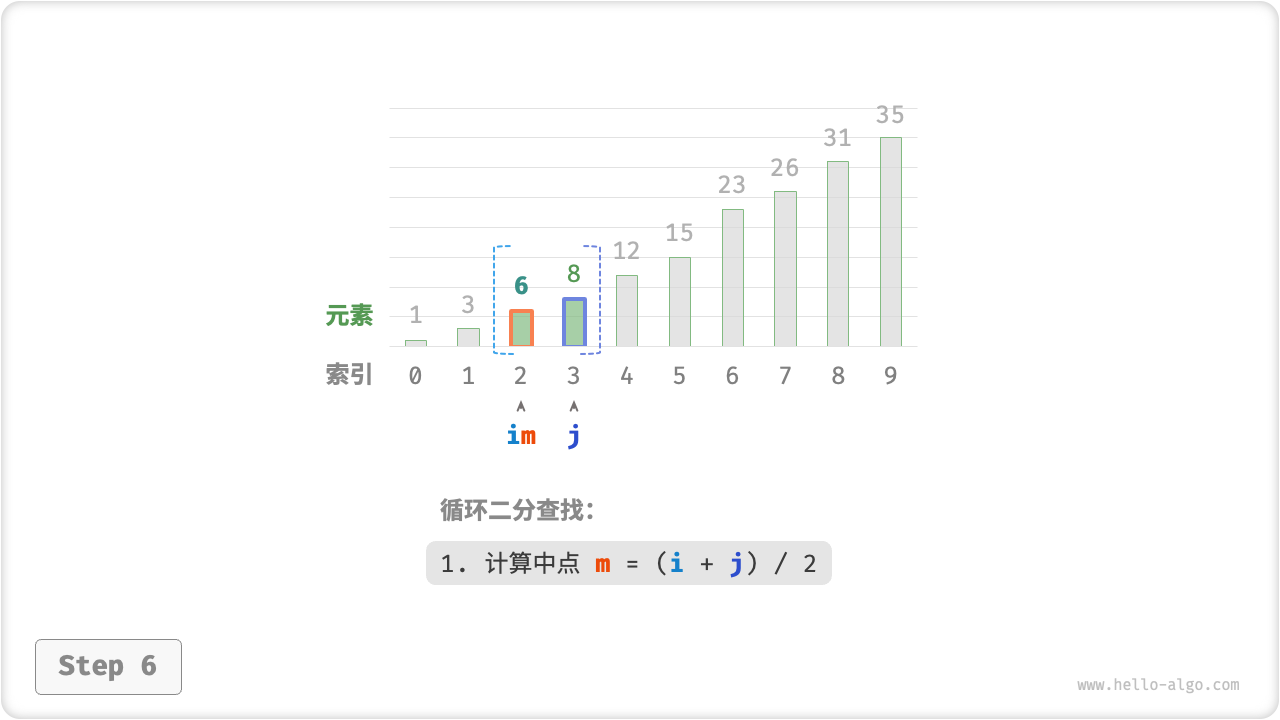

=== "<7>"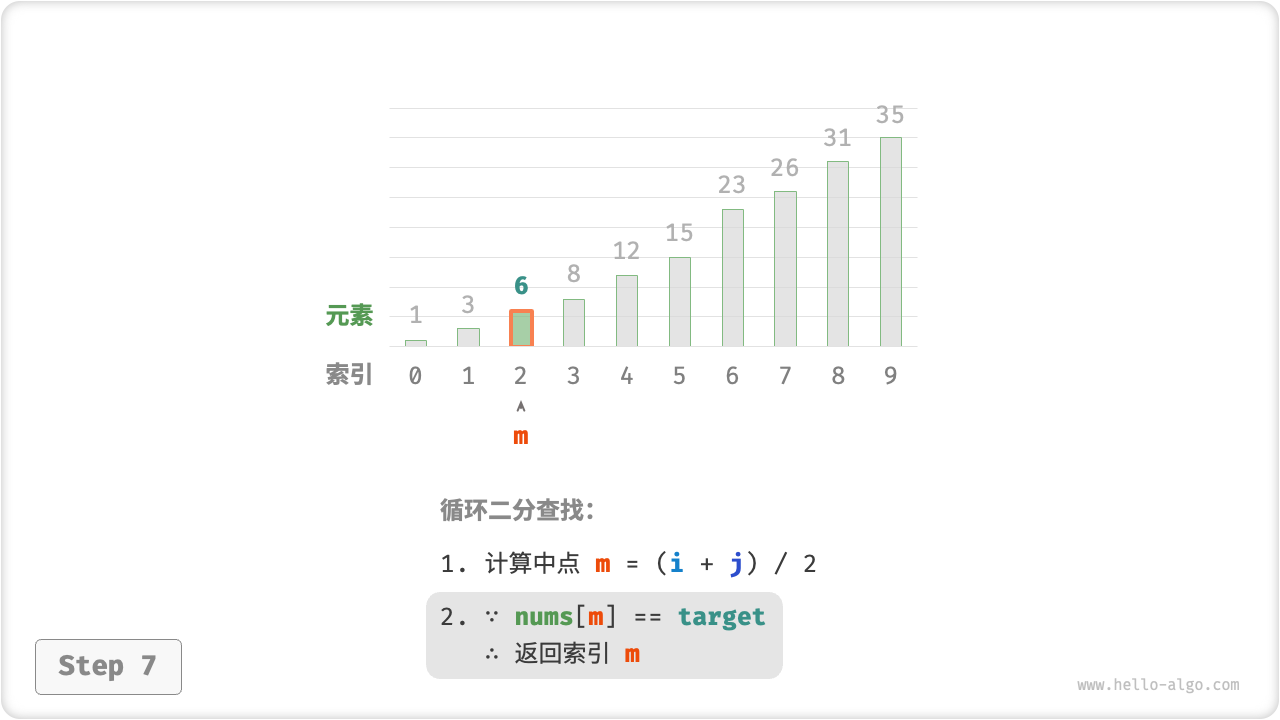

值得注意的是，由于 $i$ 和 $j$ 都是 int 类型，因此 $i + j$ 可能会超出 int 类型的取值范围。为了避免大数越界，我们通常采用公式 $m = \lfloor {i + (j - i) / 2} \rfloor$ 来计算中点。

[file]{binary_search}-[class]{}-[func]{binary_search}

时间复杂度 $O(\log n)$ ：在二分循环中，区间每轮缩小一半，循环次数为 $\log_2 n$ 。

空间复杂度 $O(1)$ ：指针 $i$ 和 $j$ 使用常数大小空间。

# 区间表示方法

除了上述的双闭区间外，常见的区间表示还有“左闭右开”区间，定义为 $[0, n)$ ，即左边界包含自身，右边界不包含自身。在该表示下，区间 $[i, j]$ 在 $i = j$ 时为空。

我们可以基于该表示实现具有相同功能的二分查找算法。

[file]{binary_search}-[class]{}-[func]{binary_search_lcro}

如下图所示，在两种区间表示下，二分查找算法的初始化、循环条件和缩小区间操作皆有所不同。

由于“双闭区间”表示中的左右边界都被定义为闭区间，因此指针 $i$ 和 $j$ 缩小区间操作也是对称的。这样更不容易出错，因此一般建议采用“双闭区间”的写法。

# 优点与局限性

二分查找在时间和空间方面都有较好的性能。

• 二分查找的时间效率高。在大数据量下，对数阶的时间复杂度具有显著优势。例如，当数据大小 $n = 2^{20}$ 时，线性查找需要 $2^{20} = 1048576$ 轮循环，而二分查找仅需 $\log_2 2^{20} = 20$ 轮循环。
• 二分查找无须额外空间。相较于需要借助额外空间的搜索算法（例如哈希查找），二分查找更加节省空间。

然而，二分查找并非适用于所有情况，主要有以下原因。

• 二分查找仅适用于有序数据。若输入数据无序，为了使用二分查找而专门进行排序，得不偿失。因为排序算法的时间复杂度通常为 $O(n \log n)$ ，比线性查找和二分查找都更高。对于频繁插入元素的场景，为保持数组有序性，需要将元素插入到特定位置，时间复杂度为 $O(n)$ ，也是非常昂贵的。
• 二分查找仅适用于数组。二分查找需要跳跃式（非连续地）访问元素，而在链表中执行跳跃式访问的效率较低，因此不适合应用在链表或基于链表实现的数据结构。
• 小数据量下，线性查找性能更佳。在线性查找中，每轮只需要 1 次判断操作；而在二分查找中，需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法（减法），共 4 ~ 6 个单元操作；因此，当数据量 $n$ 较小时，线性查找反而比二分查找更快。