二分查找边界
二分查找边界
查找左边界
注意
给定一个长度为 $n$ 的有序数组 `nums` ,数组可能包含重复元素。请返回数组中最左一个元素 `target` 的索引。若数组中不包含该元素,则返回 $-1$ 。
回忆二分查找插入点的方法,搜索完成后 指向最左一个 target ,因此查找插入点本质上是在查找最左一个 target 的索引。
考虑通过查找插入点的函数实现查找左边界。请注意,数组中可能不包含 target ,这种情况可能导致以下两种结果。
- 插入点的索引 越界。
- 元素
nums[i]与target不相等。
当遇到以上两种情况时,直接返回 即可。
[file]{binary_search_edge}-[class]{}-[func]{binary_search_left_edge}
查找右边界
那么如何查找最右一个 target 呢?最直接的方式是修改代码,替换在 nums[m] == target 情况下的指针收缩操作。代码在此省略,有兴趣的同学可以自行实现。
下面我们介绍两种更加取巧的方法。
复用查找左边界
实际上,我们可以利用查找最左元素的函数来查找最右元素,具体方法为:将查找最右一个 target 转化为查找最左一个 target + 1。
如下图所示,查找完成后,指针 指向最左一个 target + 1(如果存在),而 指向最右一个 target ,因此返回 即可。
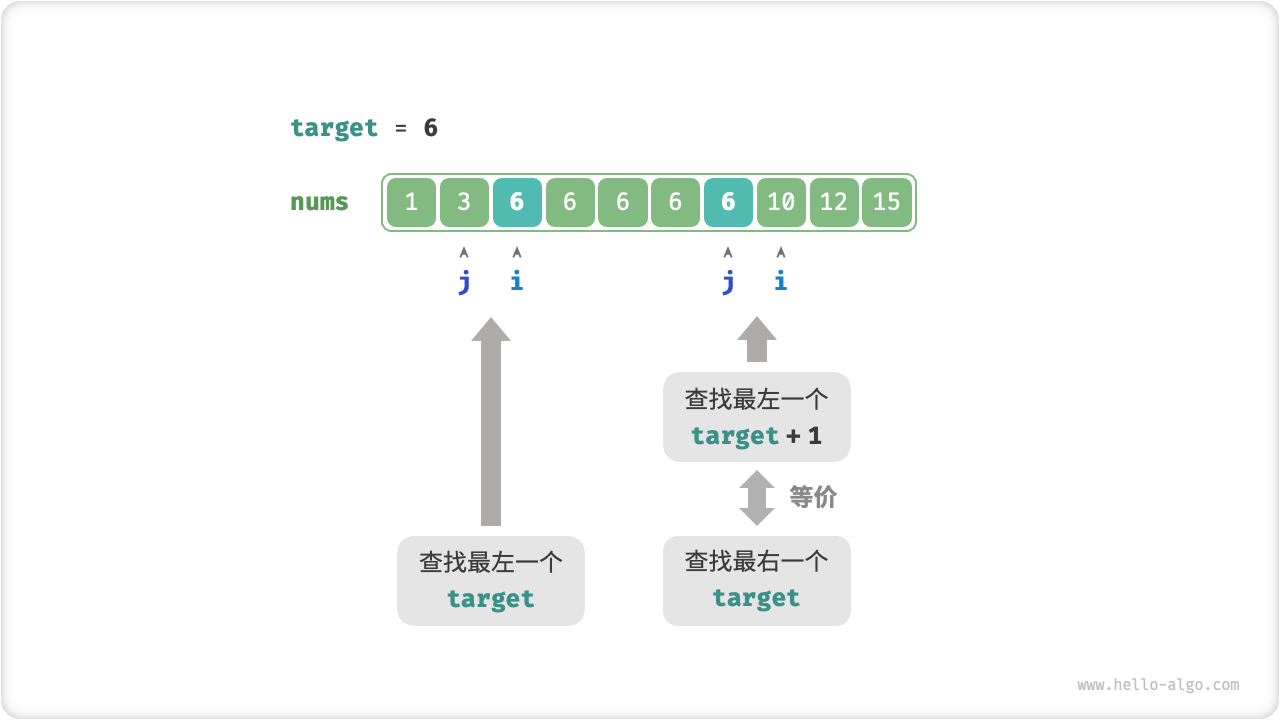
请注意,返回的插入点是 ,因此需要将其减 ,从而获得 。
[file]{binary_search_edge}-[class]{}-[func]{binary_search_right_edge}
转化为查找元素
我们知道,当数组不包含 target 时,最终 和 会分别指向首个大于、小于 target 的元素。
因此,如下图所示,我们可以构造一个数组中不存在的元素,用于查找左右边界。
- 查找最左一个
target:可以转化为查找target - 0.5,并返回指针 。 - 查找最右一个
target:可以转化为查找target + 0.5,并返回指针 。
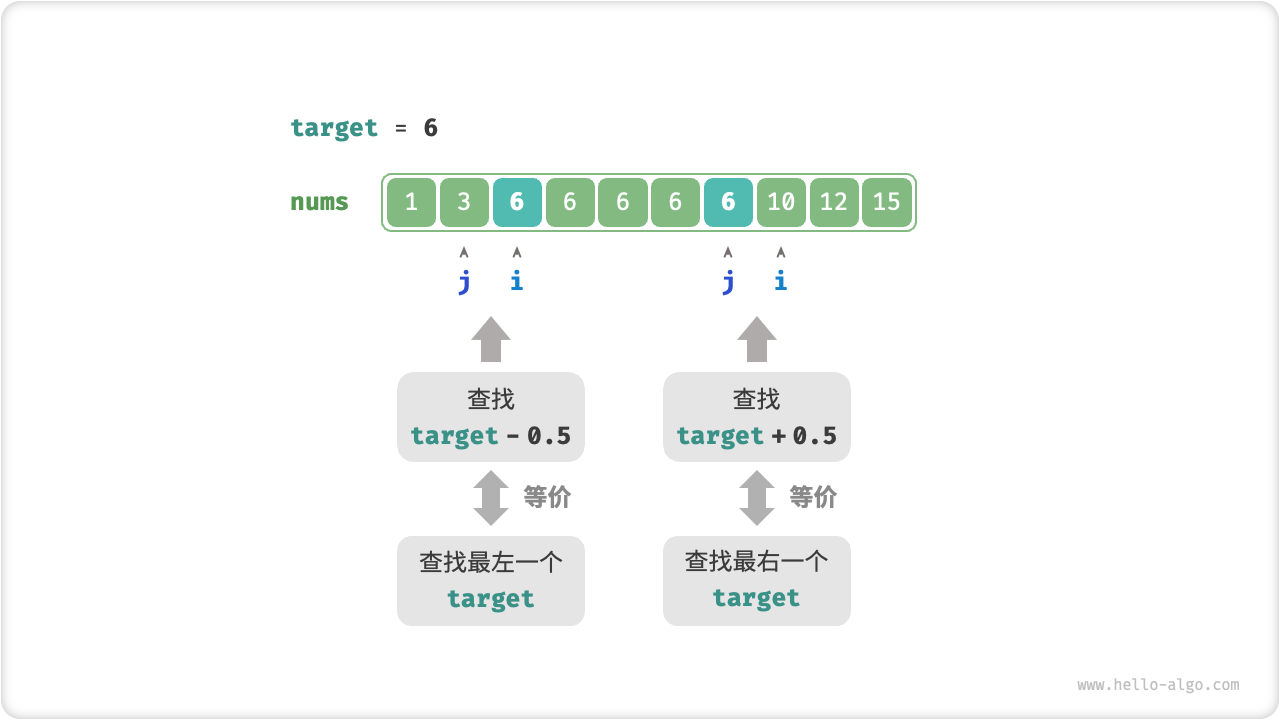
代码在此省略,值得注意以下两点。
- 给定数组不包含小数,这意味着我们无须关心如何处理相等的情况。
- 因为该方法引入了小数,所以需要将函数中的变量
target改为浮点数类型。
