哈希优化策略
哈希优化策略
在算法题中,我们常通过将线性查找替换为哈希查找来降低算法的时间复杂度。我们借助一个算法题来加深理解。
注意
给定一个整数数组 `nums` 和一个目标元素 `target` ,请在数组中搜索“和”为 `target` 的两个元素,并返回它们的数组索引。返回任意一个解即可。
线性查找:以时间换空间
考虑直接遍历所有可能的组合。如下图所示,我们开启一个两层循环,在每轮中判断两个整数的和是否为 target ,若是则返回它们的索引。
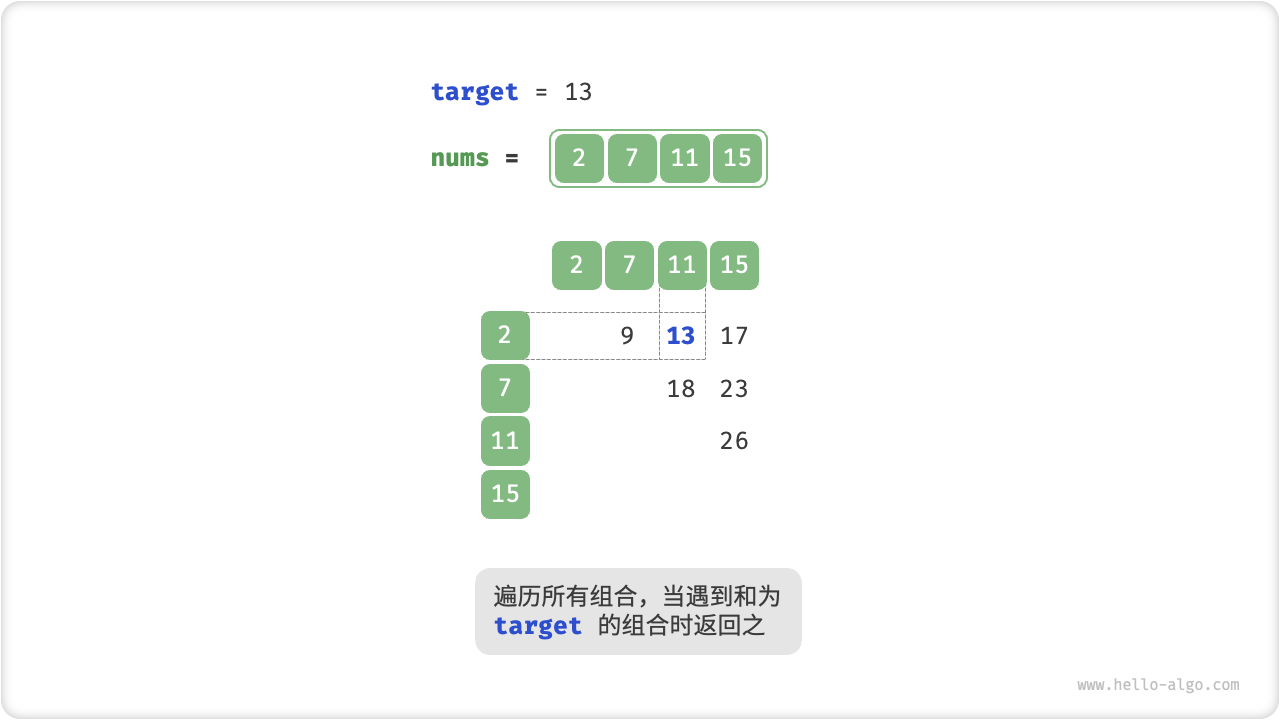
[file]{two_sum}-[class]{}-[func]{two_sum_brute_force}
此方法的时间复杂度为 ,空间复杂度为 ,在大数据量下非常耗时。
哈希查找:以空间换时间
考虑借助一个哈希表,键值对分别为数组元素和元素索引。循环遍历数组,每轮执行下图所示的步骤。
- 判断数字
target - nums[i]是否在哈希表中,若是则直接返回这两个元素的索引。 - 将键值对
nums[i]和索引i添加进哈希表。
=== "<1>"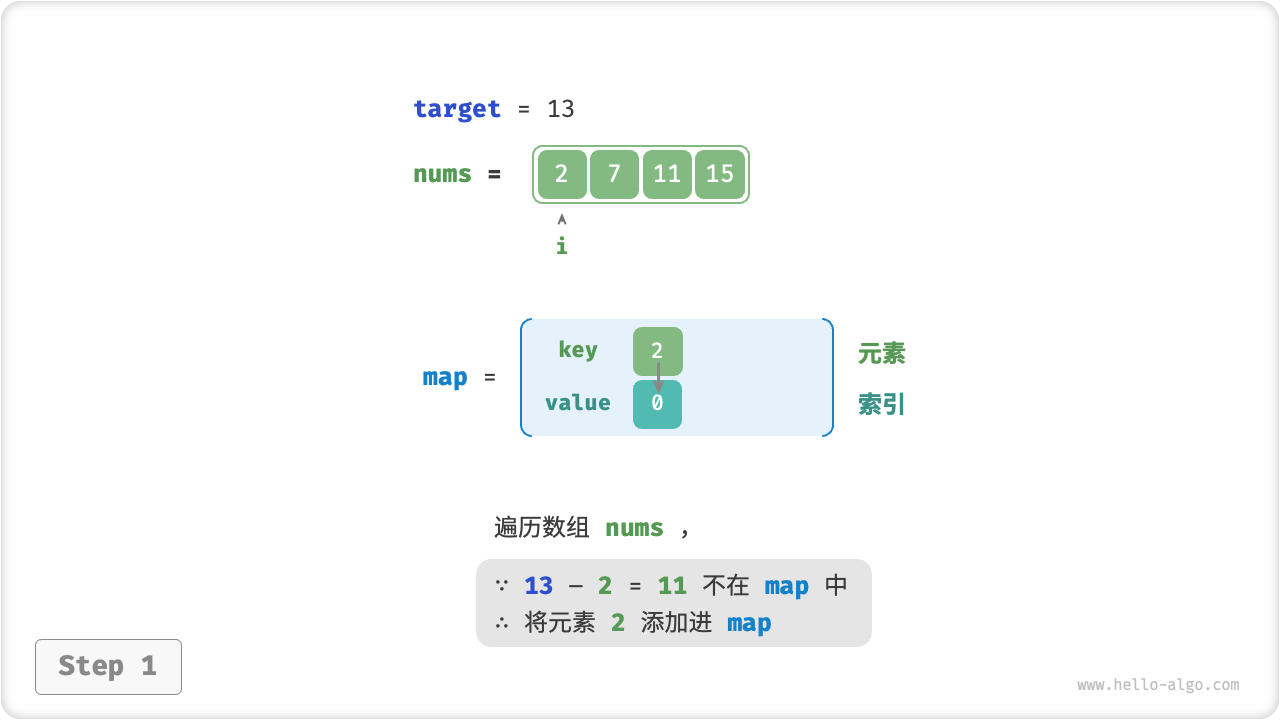
=== "<2>"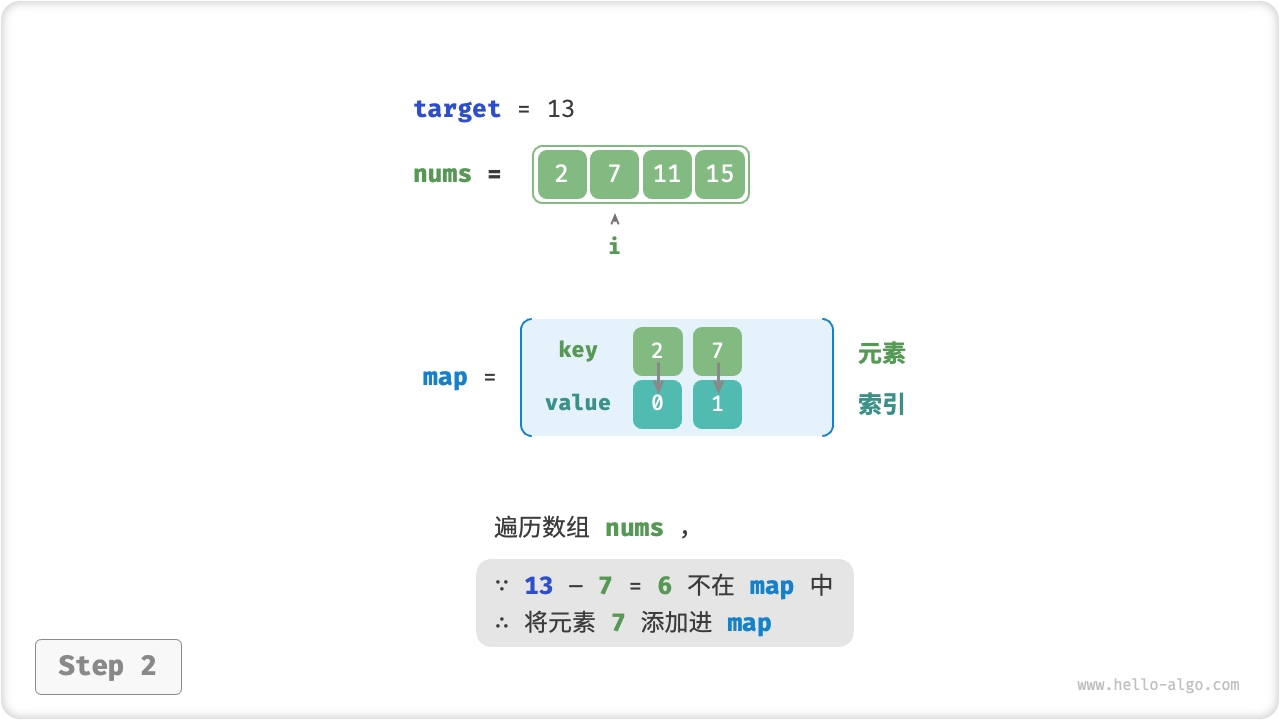
=== "<3>"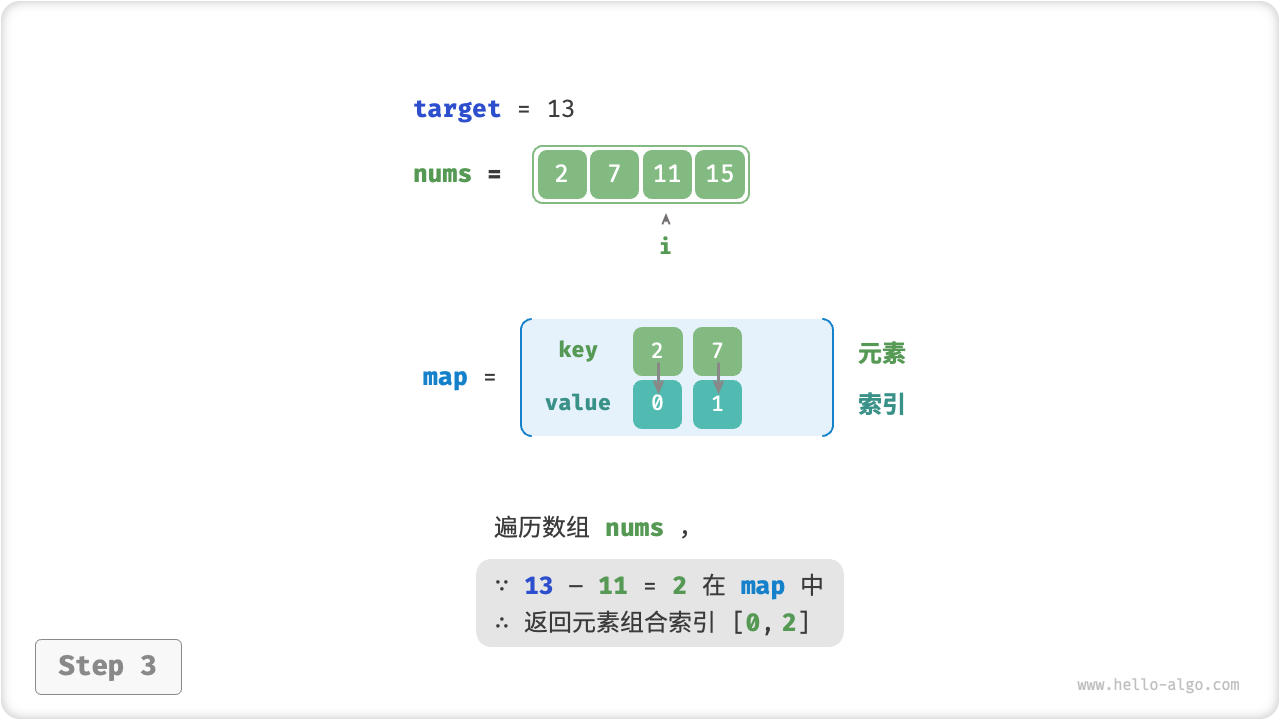
实现代码如下所示,仅需单层循环即可。
[file]{two_sum}-[class]{}-[func]{two_sum_hash_table}
此方法通过哈希查找将时间复杂度从 降低至 ,大幅提升运行效率。
由于需要维护一个额外的哈希表,因此空间复杂度为 。尽管如此,该方法的整体时空效率更为均衡,因此它是本题的最优解法。
