图基础操作

图的基础操作可分为对“边”的操作和对“顶点”的操作。在“邻接矩阵”和“邻接表”两种表示方法下，实现方式有所不同。

基于邻接矩阵的实现

给定一个顶点数量为 $n$ 的无向图，则各种操作的实现方式如下图所示。

添加或删除边：直接在邻接矩阵中修改指定的边即可，使用 $O(1)$ 时间。而由于是无向图，因此需要同时更新两个方向的边。
添加顶点：在邻接矩阵的尾部添加一行一列，并全部填 $0$ 即可，使用 $O(n)$ 时间。
删除顶点：在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况，需要将 $(n-1)^2$ 个元素“向左上移动”，从而使用 $O(n^2)$ 时间。
初始化：传入 $n$ 个顶点，初始化长度为 $n$ 的顶点列表 vertices ，使用 $O(n)$ 时间；初始化 $n \times n$ 大小的邻接矩阵 adjMat ，使用 $O(n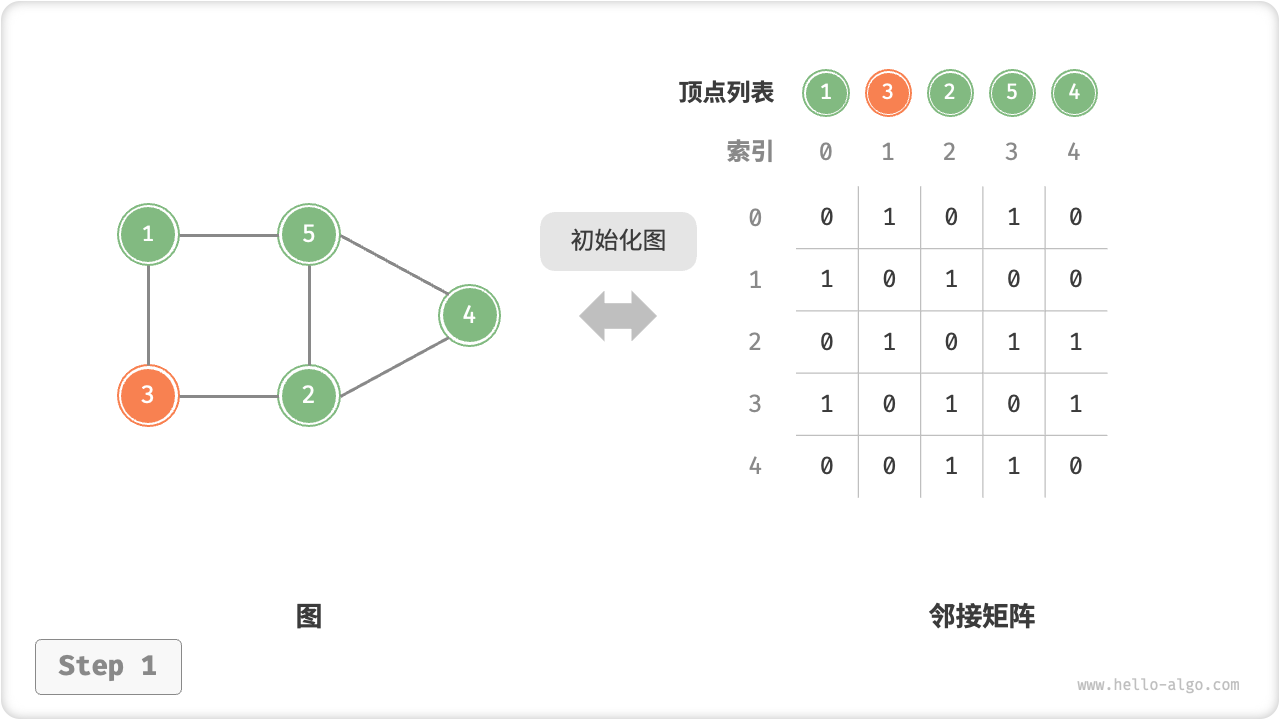^2)$ 时间。
邻接矩阵的初始化、增删边、增删顶点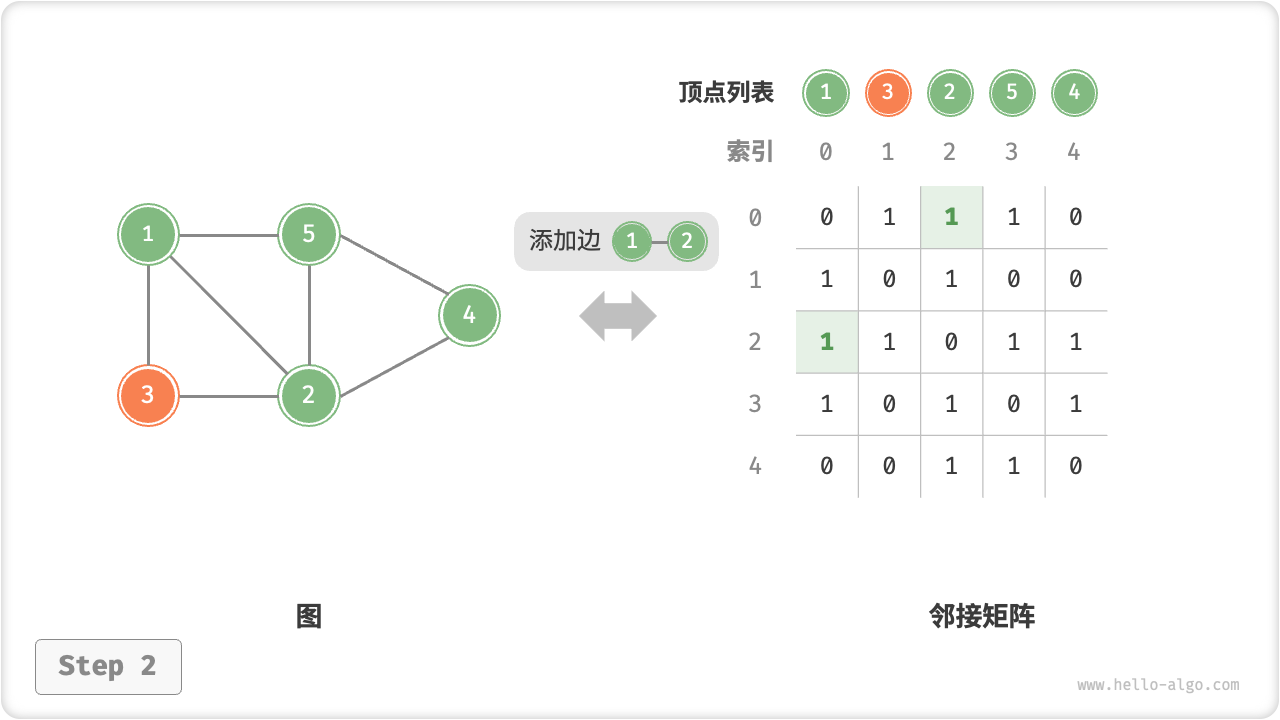
adjacency_matrix_add_edge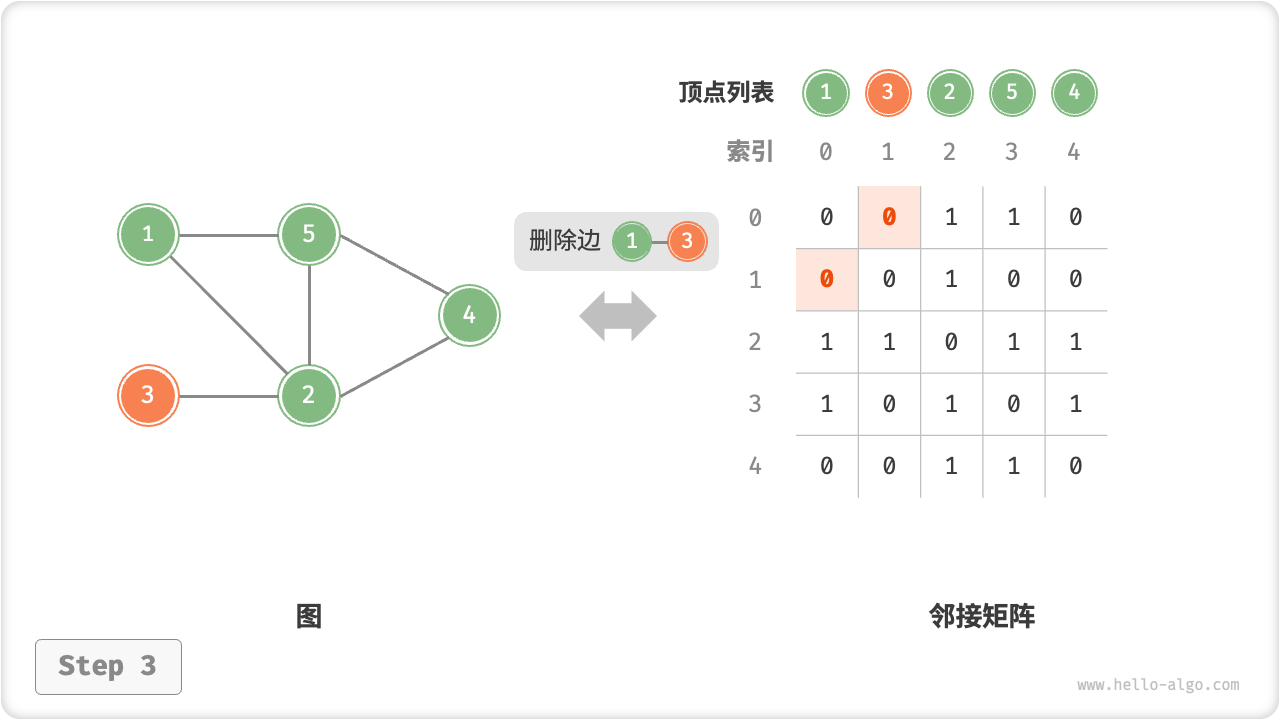
adjacency_matrix_remove_edge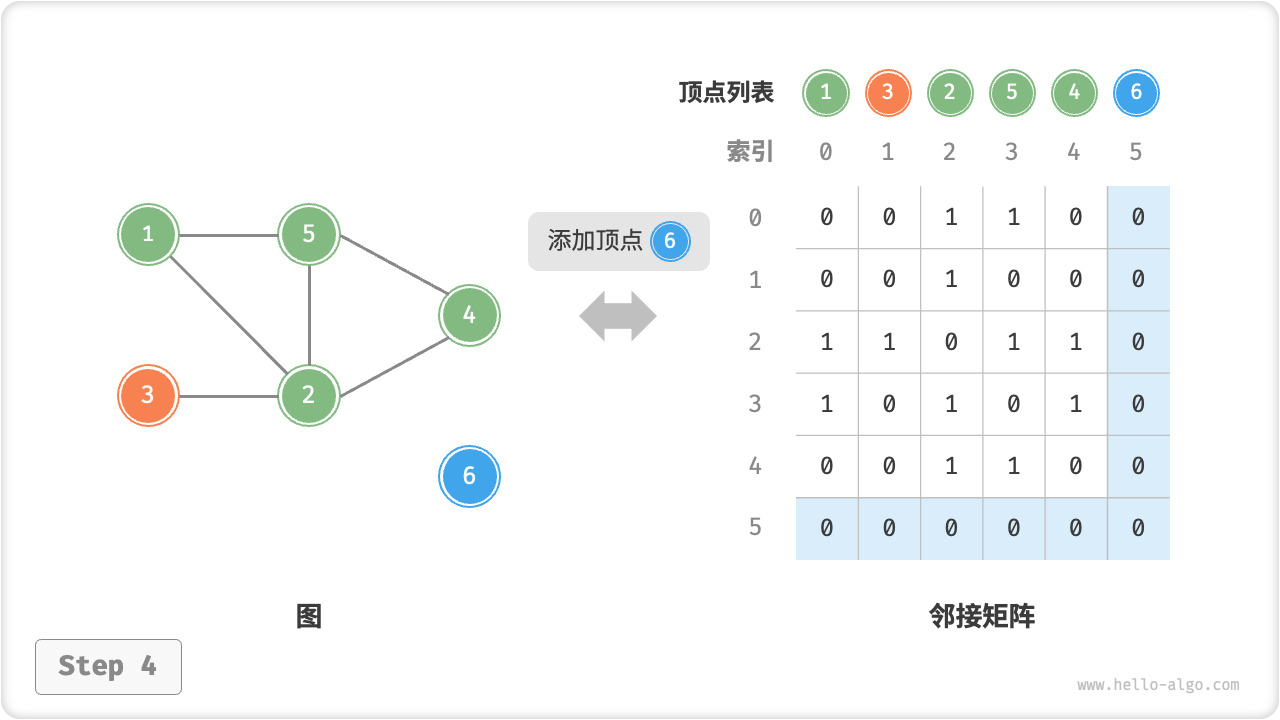
adjacency_matrix_add_vertex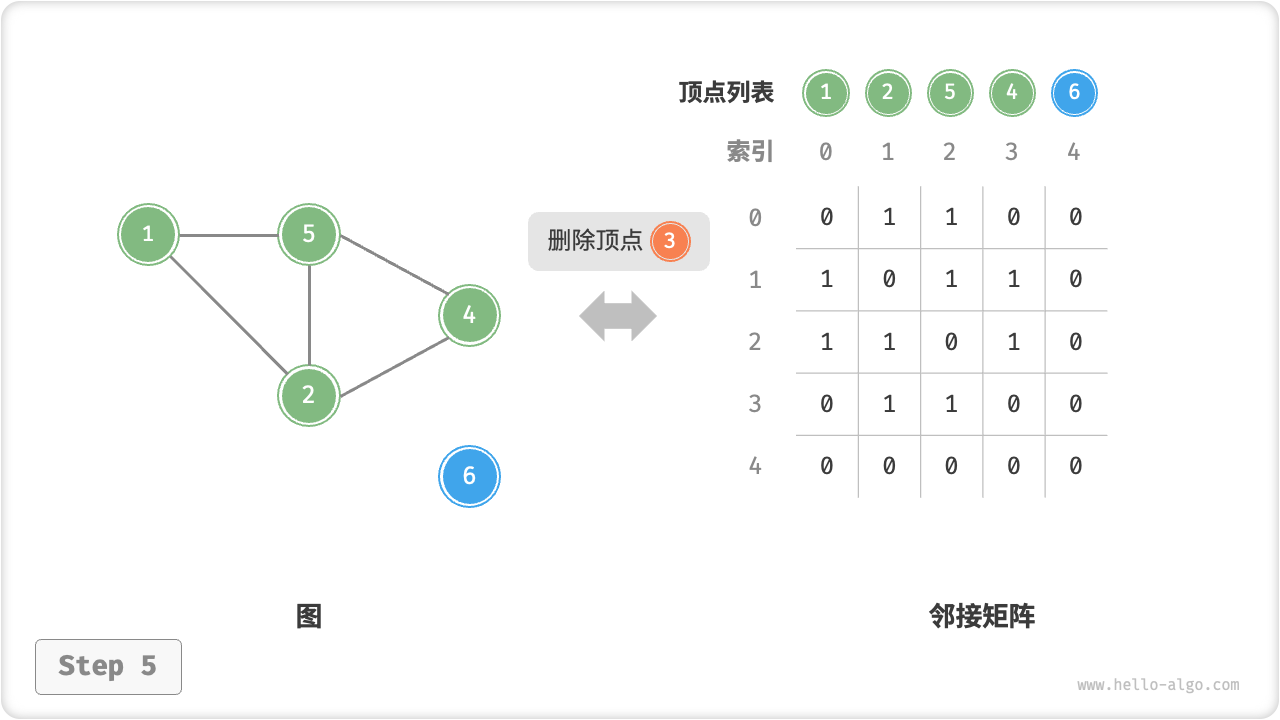
adjacency_matrix_remove_vertex

以下是基于邻接矩阵表示图的实现代码。

[file]{graph_adjacency_matrix}-[class]{graph_adj_mat}-[func]{}

基于邻接表的实现

设无向图的顶点总数为 $n$ 、边总数为 $m$ ，则可根据下图所示的方法实现各种操作。

添加边：在顶点对应链表的末尾添加边即可，使用 $O(1)$ 时间。因为是无向图，所以需要同时添加两个方向的边。
删除边：在顶点对应链表中查找并删除指定边，使用 $O(m)$ 时间。在无向图中，需要同时删除两个方向的边。
添加顶点：在邻接表中添加一个链表，并将新增顶点作为链表头节点，使用 $O(1)$ 时间。
删除顶点：需遍历整个邻接表，删除包含指定顶点的所有边，使用 $O(n + m)$ 时间。
初始化：在邻接表中创建 $n$ 个顶点和 $2m$ 条边，使用 $O(n + m)$ 时间。
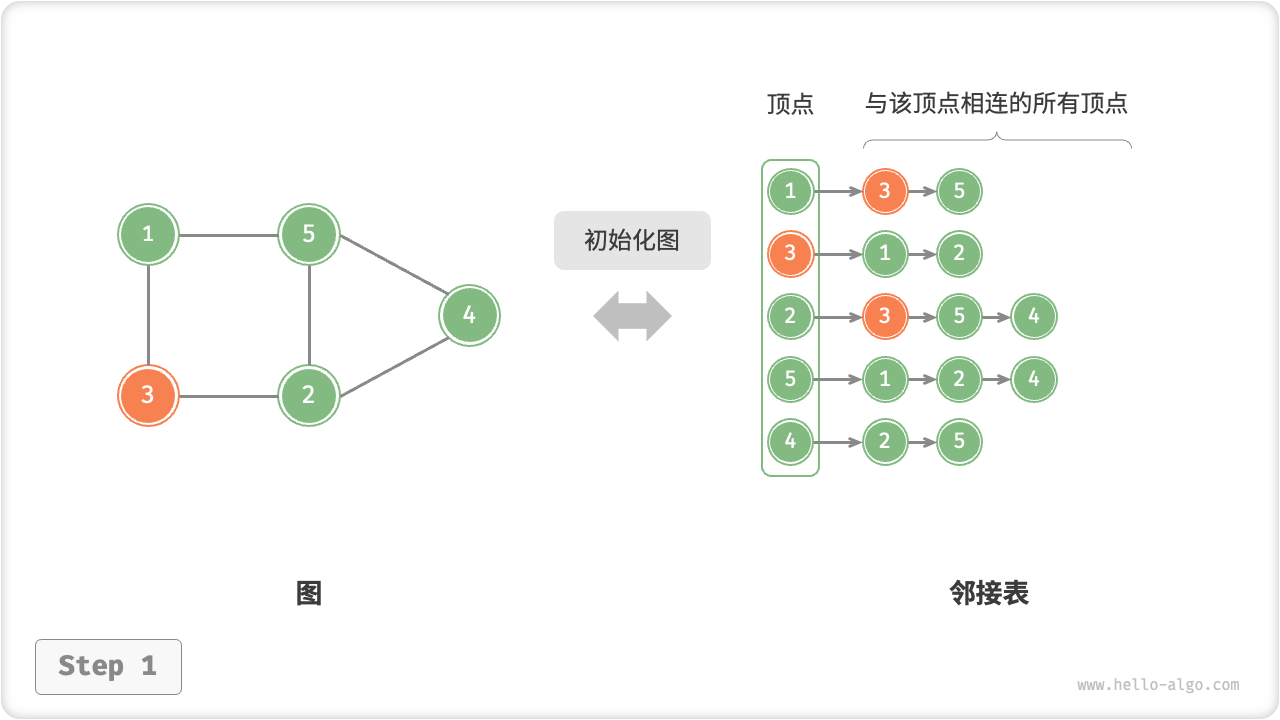
邻接表的初始化、增删边、增删顶点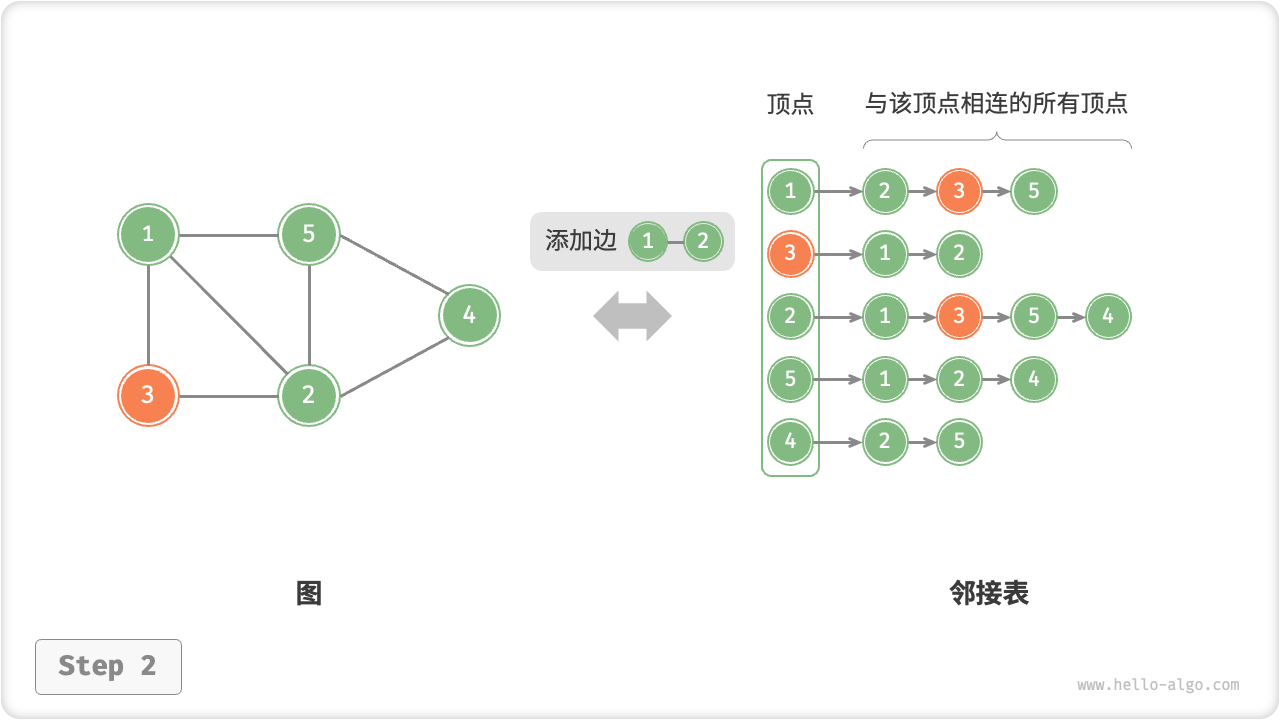
adjacency_list_add_edge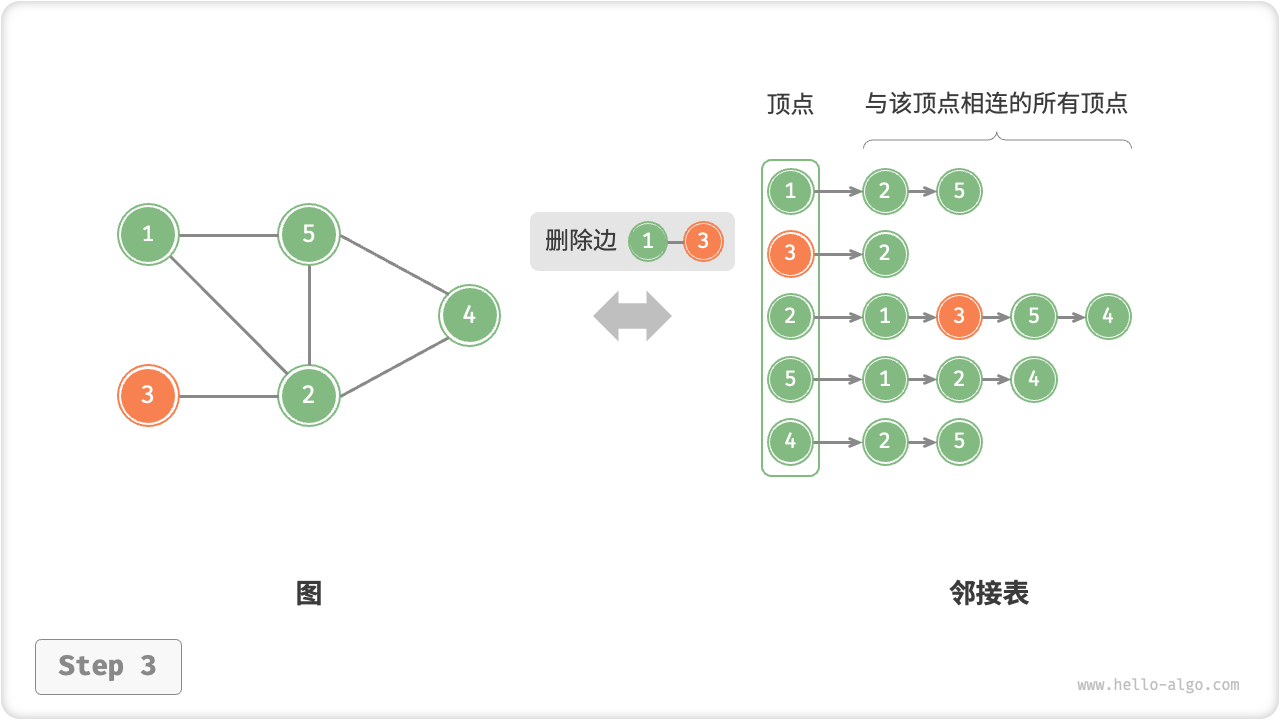
adjacency_list_remove_edge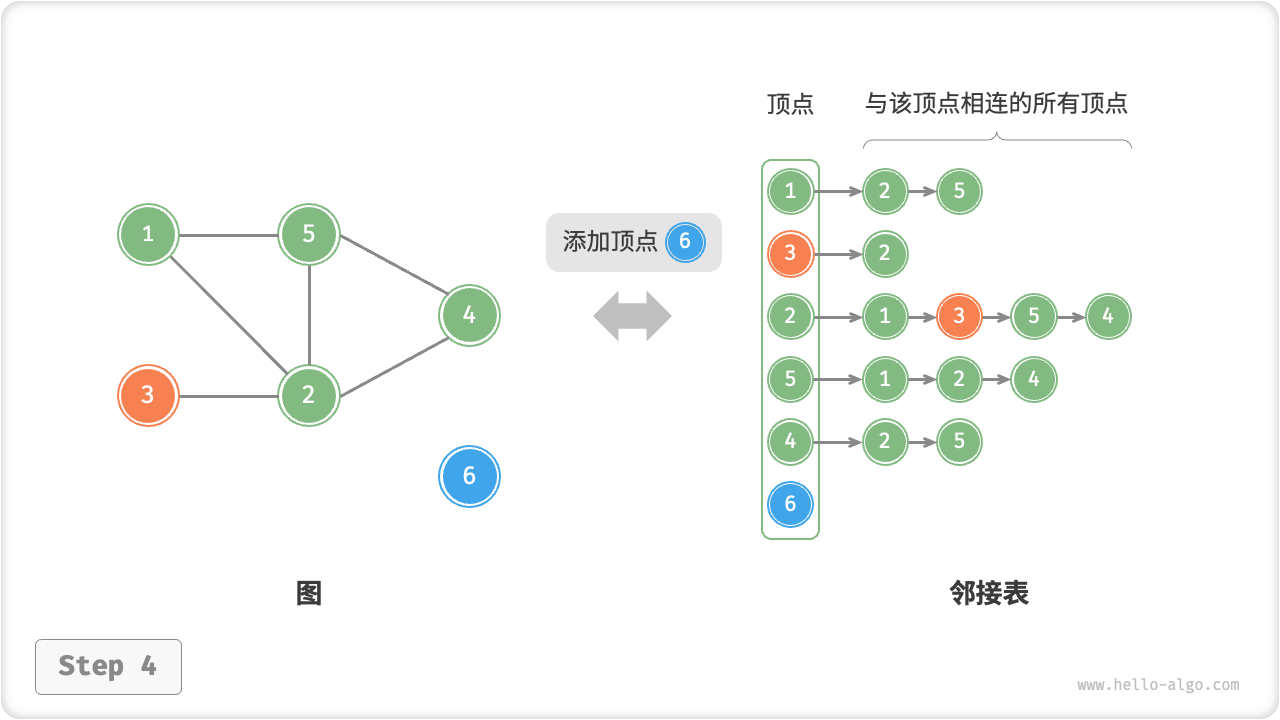
adjacency_list_add_vertex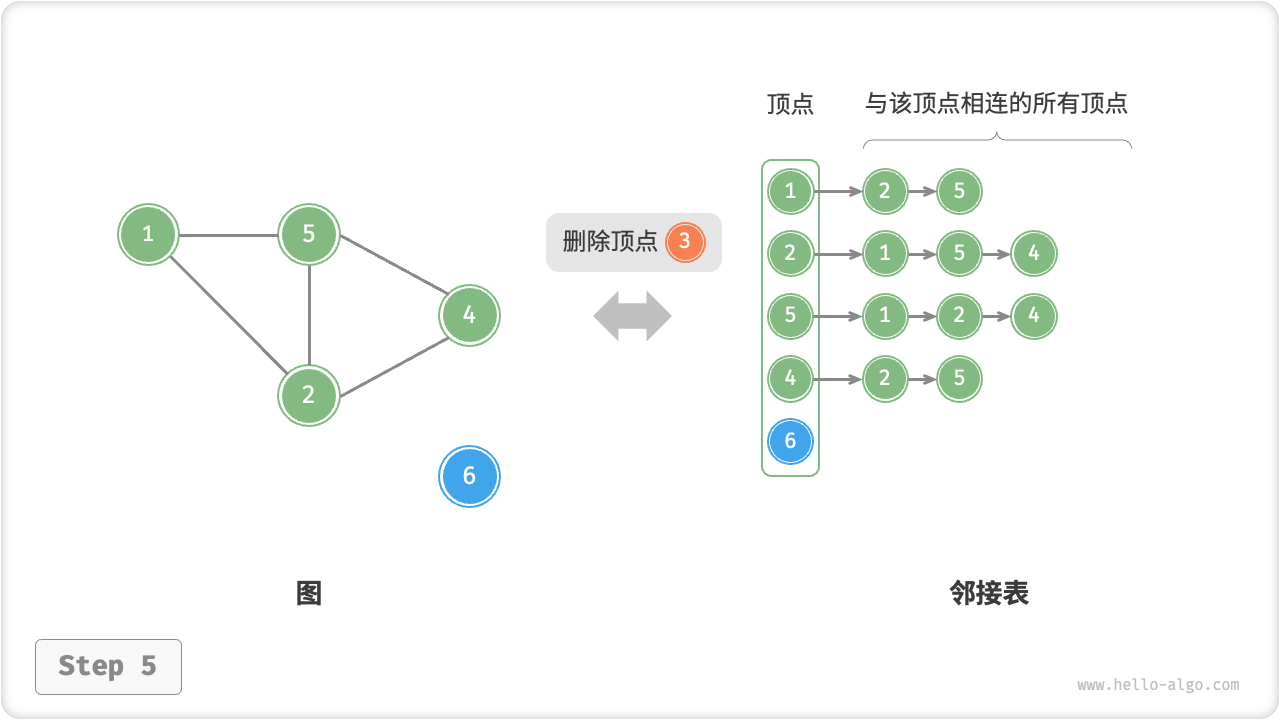
adjacency_list_remove_vertex

以下是邻接表的代码实现。对比上图，实际代码有以下不同。

为了方便添加与删除顶点，以及简化代码，我们使用列表（动态数组）来代替链表。
使用哈希表来存储邻接表，key 为顶点实例，value 为该顶点的邻接顶点列表（链表）。

另外，我们在邻接表中使用 Vertex 类来表示顶点，这样做的原因是：如果与邻接矩阵一样，用列表索引来区分不同顶点，那么假设要删除索引为 $i$ 的顶点，则需遍历整个邻接表，将所有大于 $i$ 的索引全部减 $1$ ，效率很低。而如果每个顶点都是唯一的 Vertex 实例，删除某一顶点之后就无须改动其他顶点了。

[file]{graph_adjacency_list}-[class]{graph_adj_list}-[func]{}

效率对比

设图中共有 $n$ 个顶点和 $m$ 条边，下表对比了邻接矩阵和邻接表的时间和空间效率。

表 - 邻接矩阵与邻接表对比

	邻接矩阵	邻接表（链表）	邻接表（哈希表）
判断是否邻接	$O(1)$	$O(m)$	$O(1)$
添加边	$O(1)$	$O(1)$	$O(1)$
删除边	$O(1)$	$O(m)$	$O(1)$
添加顶点	$O(n)$	$O(1)$	$O(1)$
删除顶点	$O(n^2)$	$O(n + m)$	$O(n)$
内存空间占用	$O(n^2)$	$O(n + m)$	$O(n + m)$

观察上表，似乎邻接表（哈希表）的时间与空间效率最优。但实际上，在邻接矩阵中操作边的效率更高，只需要一次数组访问或赋值操作即可。综合来看，邻接矩阵体现了“以空间换时间”的原则，而邻接表体现了“以时间换空间”的原则。

图基础操作

# 图基础操作

# 基于邻接矩阵的实现

# 基于邻接表的实现

# 效率对比

图基础操作

基于邻接矩阵的实现

基于邻接表的实现

效率对比